About

I'm a research associate at The Alan Turing Institute, working on probabilistic programming. During my PhD with Rich Turner, in the machine learning group (MLG) at Cambridge, I worked on approximate inference in Gaussian processes, how Gaussian processes they should feature in probabilistic programming, and how to scale GPs for large time series and spatio-temporal problems. Subsequently I worked on algorithmic differentiation in the Julia programming language with Hong Ge, also in the MLG.

Much of my work can be found on my github.

Research Highlights

Combining Pseudo-Point and State Space Approximations for Sum-Separable Gaussian Processes

This work shows how to combine pseudo-point (a.k.a sparse, inducing point, etc) and state space approximations for GPs – this is a good idea because they have complementary strengths and weaknesses, and combining them yields the benefits of both approximations. In this work we showed that combining them is remarkably simple, and provide straightforward-to-implement methods for approximate learning and inference. It's not a priori obvious how to do this in a principled way – and our main contribution is showing that, due to a little-known existing result, the "right" way to do this is the "obvious" one. We specifically show how to do this using the widely-favoured variational pseudo-point approximation, but our result generalises to other flavours of pseudo-point approximation. In particular, our work shines a new light on older work that constructed a very similar approximation using FITC. Appeared at UAI 2021.

Julia implementation of the technique available in TemporalGPs.jl (see examples). Code to reproduce experiments available here.

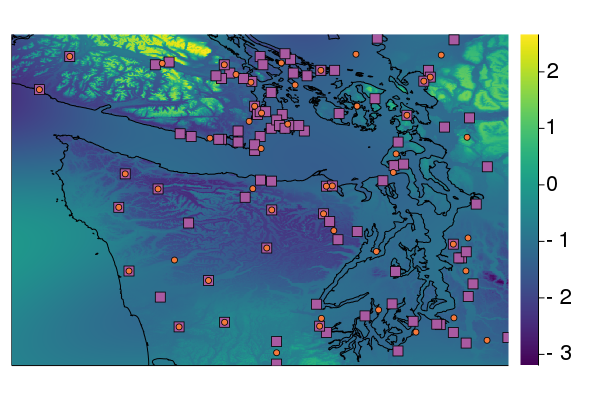
Gaussian Process Probabilistic Programming

Gaussian process probabilistic programming (GPPP) is a term I've coined for the work I'm doing to re-design the way that we work with GPs in a practical sense. I presented the high-level aspects of this work at ProbProg and JuliaCon, and continue to work on a paper.

Implementations available in Julia and Python.

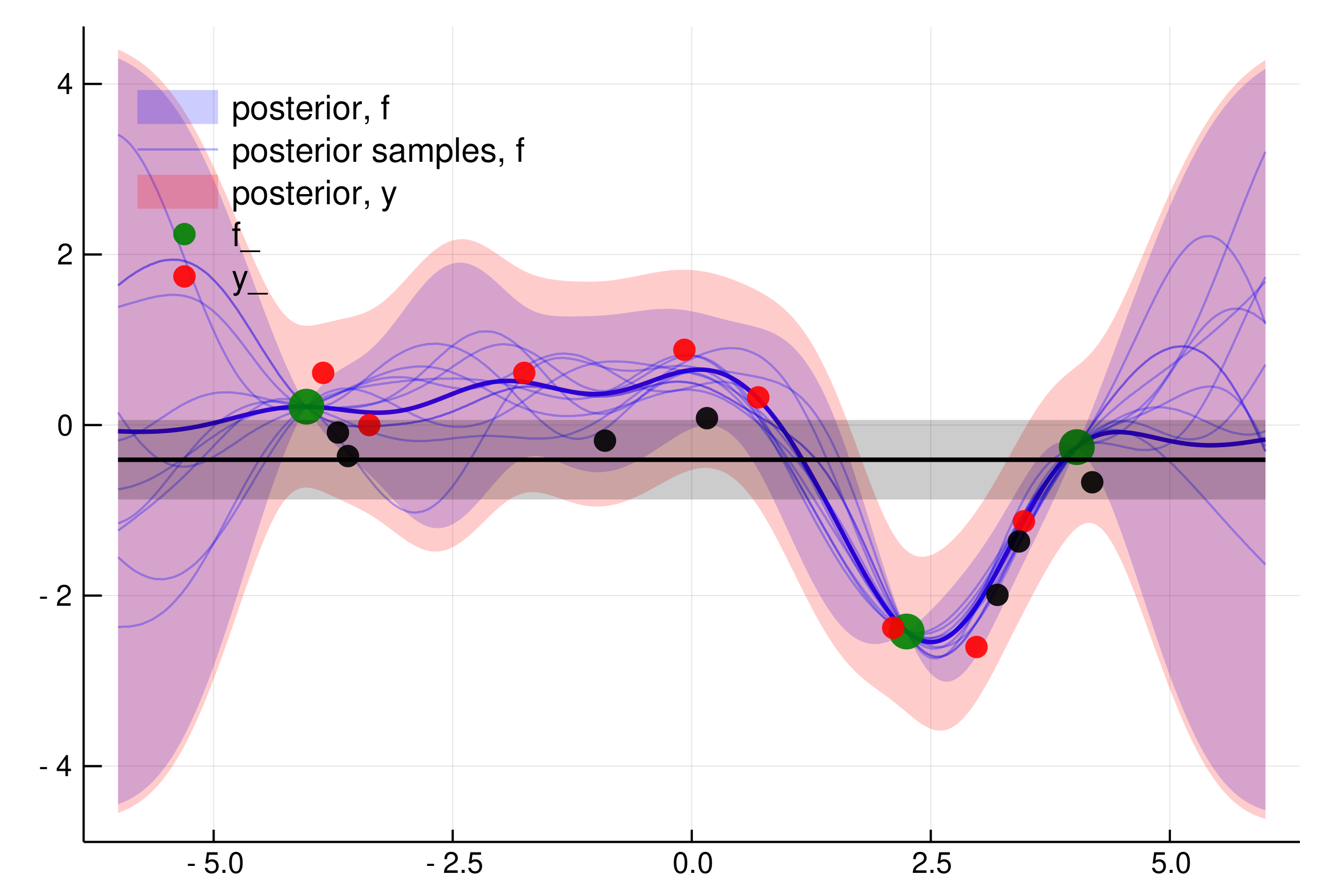
GPAR

GPAR is a multi-output Gaussian process-based regression model. It's simple, scalable by GP standards, and seems to work really well in practice. In particular it overcomes some of the limitations of standard multi-output GPs. It appeared at AISTATS 2019.

Implementations available in Python and Julia.

The OILMM

The OILMM is another multi-output Gaussian process model for regression that's easily able to handle a lot of outputs while retaining exact inference. It's really Wessel's thing – he came up with the main idea, and he and Eric did most of the work. I pointed out the connection with separable spatio-temporal processes and state space approximations, some ideas for experiments, and used TemporalGPs.jl to run one of the experiments. It appeared at ICML 2020.

Implementations available in Python and Julia.

Software

Mooncake.jl

Mooncake.jl is an AD for the Julia language that Hong and I have created. It is written entirely in the Julia programming language, while supporting much more of the language and being much more performant than any previous AD written in this way.

Stheno.jl

This is a Julia implementation of my GPPP work. It's permanently ongoing, but makes working with GPs in problems involving multiple related processes signficantly more straightforward than traditional GP packages.

JuliaCon 2019: talk and slides.

TemporalGPs.jl

This work implements SDE approximations to GPs, which dramatically accelerates inference and learning for models involving long time horizons. This is notable because the standard pseudo-point approximations fail in these scenarios.

JuliaCon 2020: talk and slides.

JuliaGaussianProcesses

The above two packages have been incorporated into the JuliaGPs organisation, which aims to unify a range of packages for GPs in the Julia ecosystem, and to provide strong foundations for research into GPs, and their use in practice.

JuliaCon 2022: talk